Eksponentinės funkcijos. Funkcija, tolydi visiems iracionaliems skaičiams, tačiau trūki visiems racionaliems. Matematika. Vartiklis

„Didžiausias žmonių rasės trūkumas yra nesugebėjimas suprasti eksponentinę fiunkciją“, Albert A. Bartlett‘as, 1976

e visad mane trikdė – bet ne raidė, o matematinė konstanta. Ką ji iš tikro reiškia?
Ji nuolat šmėžuoja kaip logaritminių ir eksponentinių funkcijų pagrindas, naudojama banko palūkanų, radioaktyvaus skilimo, akumuliatorius išsikrovimo laiko ir pan. paskaičiavimams.

Kasdieniniame gyvenime žodžiu „transcendentinis“ paprastai suvokiama kažkas, kas yra už kasdienybės ribų, tačiau matematikoje jo prasmė labiau kasdieniška – šiuo terminu paprasčiausiai nusakoma begalinė aibė skaičių, negalinčių būti polinominių lygčių (pvz., ax³ + bx² + cx + d = 0) šaknimis (t.y. sprendiniais) ir kaip L. Oileris išsireiškė: „Jie transcendentuoja algebrinių metodų galią“.

Tačiau šis apibūdinimas „transcendentinis“ taikomas ir dviem universaliausioms konstantoms p ir e - visuotinai naudojamas, be galo mįslingas ir vos ne magiškas. Iš jų, p yra žinomesnė mums ir vos ne kiekvienas žino jos apytikslę reikšmę (3,14..., skaitykite apie p istoriją). Antroji, Oilerio skaičius, esanti natūralių logaritmų pagrindu, apytiksliai lygi 2,7 1828 1828 4590 45... (šią dalį santykinai lengva įsiminti), tačiau būtent jos transcendentalumas buvo pirmąkart įrodytas (Š. Ermitas 1873-ais). Ji turi keletą unikalių savybių (skaitykite, pvz., Kirmgrauža tarp matematikos sričių).

Oficialus apibrėžimas yra nuobodus:
e - konstanta (kartais dar vadinama Oilerio skaičiumi arba Neperio konstanta) yra natūralaus logaritmo funkcijos pagrindas, kurio apytikslė reikšmė yra
2.718281828459045235360287471352662497757247093699959574966967627724076630353547594571382178525...
Dar bandoma ją apibrėžti per sekos ribą, per begalinės eilutės, sumuojančios atvirkštinius faktorialus, sumą, per integralo reikšmę...

Tačiau e nėra vien tik skaičius. Iš tikro e yra didėjimo sparta bendra visiems tolygiai greitėjantiems procesams. Ji parodo, ar sistemos keičiasi eksponentiškai: populiacijos pokytis, radioaktyvus skilimas, ... Štai keli pavyzdžiai sistemų, kuriose kažkas padvigubėja per laiko intervalą:

Po n padvigubėjimų mes turime 2ⁿ pradinių objektų; arba, perrašius kitaip, (1+100%)ⁿ. Panašiai, vietoje 100% mes galime įrašyti bet kurią kitą reikšmę ir gausime augimo formulę tai naujai spartai, t.y. (1+sparta)ⁿ. Pvz., jei mes investavome 1 eurą su 10% palūkanomis, tai po 10 m. jis mums gražins (1+10%)¹⁰ euro, t.y. apie 2,6 Eur. Eksponentinis kitimas

Šioje formulėje kitimai vyksta diskrečiais žingsniais. Visos bakterijos laukia, o tada visos kartu staiga skyla. Mūsų pelnas stebuklingai padvigubėja praėjus tiksliai metams ir t.t. Tačiau realiame pasaulyje taip nevyksta. Juk kai tik mes uždinbome centą, tas centas gali pradėti uždirbinėti naujus centus.

Imkim pavyzdį, kai per metus uždirbame 100% pradinio kapitalo. Tada per pusę metų, uždirbsime 50%, o per kitą pusmetį – kitą 50%. Taip galime dalinti į 3,4,5,… dalis – tada per n periodų gausim grąžą lygią (1+100%/n)ⁿ. Ir kai n artėja į begalybę, gauname ribinę reikšmę, apytiksliai lygią 1,718…, t.y. e:

e yra maximali įmanoma grąža turint 100% augimo spartą per tam tikrą laiko intervalą. Tarkim, pradedam su 1 Eur. Po metų galim tikėtis 2, tačiau, jei metus dalijame pusiau, tai įdarbinę pusmečio „dividendus“, per metus gausime … 2,25. O jei dalintume į ketvirčius, tai metai mums atneštų jau 2,44, o jei pamėnesiui – 2,61… ir kuo smulkesnis padalijimas, tuo labiau įdarbijami mikrodividendai, tuo metinė grąža artimesnė e.

Bet grįžkim prie ankstesnio pavyzdžio su 10% palūkanomis. Maksimali grąža šiuo atveju būtų (1+0,1/n)ⁿ, o tai lygu e^0,1, t.y. e^sparta. O per 2 m. - e^2*sparta.

Pavyzdys iš tikimybių teorijos: žaidžiant ruletę ir kaskart statant tą patį numerį, tikimybė, kad pralošite visus iš 37-ių žaidimus, yra 1/e.

Kaip atsirado e?

17 a. škotų matematikas Dž. Neperis^*) ieškojo paprastesnio būdo didelių skaičių daugybai, atskiru atveju – laipsnių. Ir nors jis neatrado e, tačiau gavo logaritmų, kuriuos paskaičiavo naudodamas e jam pačiam to nežinant, sąrašą. Tai jis paskelbė „Mirifici Logarithmorum Canonis Descriptio“ (1614). Tik po 70 m. logaritmų sąrašas buvo susietas su eksponente: 1683 m. šveicarų matematikas Jakobas Bernulis atrado e, kai sprendė uždavinį, susijusį su palūkanomis. Jis ją užrašė kaip ribą:
E riba

Ir galiausiai L. Oileris suteikė e pavadinimą ir įrodė jo iracionalumą.

^*) Džonas Neperis (John Napier of Merchiston, 1550-1617) – škotų matematikas, fizikas ir astronomas. Plačiausiai žinomas už logaritmų atradimą; taip pat išrado Neperio lazdeles, kurias dėliojant pagal tam tikras taisykles, gaunama skaičių sandauga. Pirmasis paskelbė logaritmų lenteles. 1560 m. Škotijoje, po atkaklios kovos, įsigalėjo protestantiškoji Reformacija. Neperis, karštai tikintis puritonas, laiką leido užsiimdamas teologija, astrologija ir su ja susijusiais matematiniais paskaičiavimais. Anot jo, Biblijos pranašysčių aiškinimasis visad buvo pagrindiniu jo užsiėmimu, o matematika jam tebuvo poilsiu. Vis tik liko žinomas dėl „poilsio darbų“.
Dž. Neperis rimtai domėjosi astrologija ir juodąja magija. Savo knygoje „Kruvinasis almanachas“ jis patalpino gremėzdiškus paskaičiavimus, pagal kuriuos pasaulio pabaiga turėjo būti 1698-1700 m. Ir nekeista, kad tais laikais jo prognozės buvo populiaresnės už jo matematinius pasiekimus.
Jo garbei pavadintas krateris Mėnulyje ir asteroidas nr. 7096.

Funkcija, tolydi visiems iracionaliems skaičiams, tačiau trūki visiems racionaliems

Apibrėžkime funkciją f(x) taip:
f(p/q)=1/q, jei p/q yra racionalus skaičius su mažiausiais nariais, o q>0;
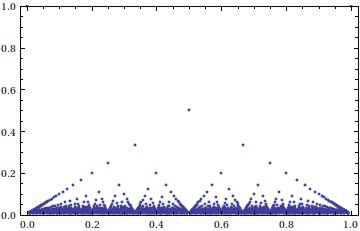
f(x)= 0, kai x yra iracionalus skaičius. Žvaigždžių virš Babilono funkcija

Kartais ši funkcija vadinama „liniuote“, nes jos grafikas primena liniuotės sužymėjimą. O jos nepaprasta savybė yra ta, kad ji yra tolydi visiems iracionaliems skaičiams, tačiau trūki visiems racionaliems skaičiams. Jos trūkumas gana akivaizdus, tačiau jos tolydumą sunkiau įrodyti. Kalbant vaizdžiai, racionalūs skaičiai negali priartėti prie iracionalaus x kitaip, nei jų vardikliui artėjant į begalybę, tam, kad f artėtų prie 0.

Formaliai. Paimkim bet kokį e>0. Tada egzistuoja sveikas skaičius q toks, kad 1/q < e. Panagrinėkime visus racionalius skaičius p/q!. Kadangi x yra iracionalus, jis negali būti lygus nė vienam šių skaičių. Iš to, kaip p/q! išsidėstę tarp skaičių (p=0, 1, 2, …), toje sekoje yra skaičius, kuris yra arčiausia x (kad tai įrodytume, turime pasinaudoti sveikų skaičių savybėmis). Imkim d>0, kuris yra mažesnis nei to nario atstumas nuo x. Tada atstumu d nuo x negali būti jokio racionalaus skaičiaus, kurio vardiklis būtų mažesnis ar lygus q, tad visų skaičių, esančių mažesniu už d atstumu nuo x, funkcijos reikšmės bus mažesniu atstumu nei e nuo f(x), taigi f(x) yra tolydi kiekvienam iracionaliam skaičiui.

Pastaba. Ši funkcija turi daugelį pavadinimų. Ji vadinama kukurūzų spragėsių, suskaičiuojama debesų, liniuotės, Rymano, žvaigždžių virš Babilono funkcija. Tačiau oficialiai tai Tomo funkcija (Karlo Johano Tomo garbei). Ji yra atskiras Dirichlė funkcijos variantas (Dirichlė funkcijos reikšmės yra lygios 1 racionaliems skaičiams ir 0 – visiems kitiems.

Paimkime paprastą funkciją: y=1/x

Tada grafiko dalį intervale [1, µ ] sukite aplink x ašį.
Gausite figūrą, panašią į piltuvėlį ar trimitą (kaip jums labiau patinka):
Gabrieliaus ragas

Ji vadinama Toričelio trimitu arba (arkangelo) Gabrieliaus ragu (trimitu) ir pasižymi neįtikėtina savybe: yra baigtinio tūrio, bet turi begalinį plotą. Ją 17 a. pirmasis tyrinėjo E. Toričelis.

Paradoksas yra tame, kad į piltuvėlį telpa baigtinis kiekis dažų, tačiau tų dažų nepakanka nudažyti jo sienelėms. Atrodytų, kad čia nėra jokio paradokso, bet esmė tame, kad nudažymas nėra vien dvimatis dalykas - dažų sluoksnis turi storį. gausime, jei imsime bet kokį fiksuotą sluoksnio storį – tada nuo kažkurios vietos nudažymui reikalingas dažų sluoksnis netilps į piltuvėlį (viršys jo skersmenį). Tačiau net ir šiuo atveju neatrodo, kad yra prieštaravimas – juk galime imti „be galo plonėjantį“ sluoksnį. Paradoksą išsprendžia dažymo būdas: kuo giliau į piltuvėlį, tuo plonesnis dažų sluoksnis.