Skaičiai apžvalga/ pradmenys
Vokiečių matematikas Leopold Kronecker (18231891)
Papildomai skaitykite Skaičiaus koncepcija

Paukščiai teturi tik po tris pirštus ant kojų, tad jiems turėtų būti sunku suskaičiuoti daugiau nei tris daiktus, tarkim, jie sunkiai turėtų skirti 4 ir 5 kiaušinius lizde, tačiau jame palikus tik 2 ar 3, jie pastebėtų tai. Paukščiai skaičiuotų taip: 1, 2, 3, daug...
Žmonės ant abiejų rankų turi 10 pirštų netgi sako, kad iš tai ir gimė dešimtainė skaičiavimo sistema.
Tačiau viena ranka teturi 5 pirštus, o tai leidžia turėti ir penkiatainę skaičiavimo sistemą, pvz., 13-a būtų 2
rankos ir 3 pirštai, t.y. 1310=235
Taigi, kai jau turime ir ant pirštų suskaičiuojamus (natūralius) skaičius, jiems galime taikyti aritmetinius veiksmus sudėtį, atimtį, daugybą ir dalybą. Šių veiksmų pagalba galime sukurti naujus skaičius. Tiesa, dar turėjo gimti geniali nulio (kaip skaičiaus) idėja (ir čia tai jau tikrai be Dievo pagalbos nebuvo apsieita... )
Taip, atėmus iš mažesnio skaičiaus didesnį skaičių gauname neigiamus skaičius (kurie, vis tik, dar yra sveikieji skaičiai).
Dalinant sveikus skaičius, gauname racionalius skaičius, kitaip tariant trupmenas. O dalyba iš
nulio duoda mums begalybės sampratą.
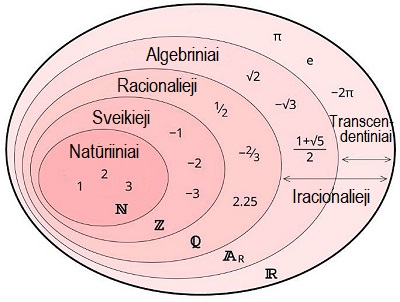
O p gaunamas apskritimo ilgį dalijant iš skersmens ir taip
gaunam iracionalius skaičius, kuriuos taip pat galima gauti ir traukiant kvadratinę šaknį iš kai kurių sveikųjų skaičių
(kada jie atsirado?). Manoma, kad juos atrado Hipasas, - ir tas atradimas kainavo jam gyvybę
(žr. >>>>>).
Sveikieji, racionalūs ir iracionalūs skaičiai visi kartu sudaro realiuosius skaičius. Geometriškai jie sudaro tiesę:
![]()
Taip pat skaitykite apie transfinityvius skaičius...
Ir jei dabar pabandysime ištraukti kvadratinę šaknį iš neigiamų skaičių, gausime menamus skaičius (kompleksinius).
Pirmąkart terminą kompleksinis pasiūlė L. Karnotas (1753-1823).
Tačiau dar 1545 m. Dž. Kardanas išleido knygą apie kubinių lygčių sprendimą
panaudojant menamą skaičių i, turintį nepaprastą savybę:
I2=-1
a+bi pavidalo kompleksiniai skaičiai palaipsniui tapo pripažintais, tačiau žmonės tebebuvo susirūpinę:
Ar i iš tikro egzistuoja? Jei taip, tai koks jis?
Ir kai sudauginame du teigiamus menamus skaičius gauname neigiame realųjį skaičių. Ir tai yra toji priežastis, kuri erdvėlaikyje neleidžia judėti
didesniu už šviesą greičiu. Štai ką padarė žmogus,
 iš Dievo gavęs skaičius (pirštus ir nulį).
iš Dievo gavęs skaičius (pirštus ir nulį).
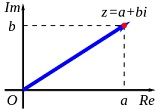
1806 m. Ž. Arganas*) pademonstravo, kad kompleksinius skaičius galima pavaizduoti taškais plokštumoje.
Realieji skaičiai išsidėstę vienoje skaičių tiesėje. Kvadratinės šaknys iš neigiamų realiųjų skaičių išsidėstę
menamoje skaičių tiesėje. Realiųjų ir menamųjų skaičių sudėtis sukuria skaičius, išsidėsčiusius kompleksinių skaičių plokštumoje.
Skaičiaus padauginimas iš a+bi tiesiog reiškia vektoriaus pasukimą ir jo ilgio pakeitimą. Tad bet kurį skaičių galima
padalinti iš nenulinio kompleksinio skaičiaus tiesiog atstatant daugybos atliktą pasukimą ir ilgio pakeitimą.
Kaip pritaikomi kompleksiniai skaičiai?
Visų pirma, kompleksiniai skaičiai supaprastina 2D analitinę geometriją. Analitinės geometrijos ištakos siekia 17 a., kai R. Dekartui kilo didi idėja plokštumos taškams priskirti koordinates (žr. Dekarto koordinatės). Dabar tai atrodo trivialu, tačiau tada tai buvo didelis šuolis matematikoje: buvo sujungtos dvi, iki tol buvusios atskiromis, sritys.
Taigi, analitinė geometrija davė naują patogų įrankį kol užsiimate taškais ir tiesiniais objektais. Reikia patikrinti, ar dvi atkarpos lygiagrečios?! Paprasta! Reikia rasti dviejų tiesių susikirtimo tašką?! Juokų darbas! Objekto sukimas aplink tašką? Įmanoma, tačiau skausminga. Kai tik imatės kampų ir sukinių, reikalai pakrypsta į gremėzdišką pusę. Iš dalies tai todėl, kad nematote tiesioginio sąryšio tarp koordinačių ir kampų.
Tačiau viskas pasikeičia, kai sužinote, kad kompleksinė plokštuma yra izomorfinė įprastai Dekarto plokštumai. Todėl analitinėje geometrijoje vietoje taško pavaizdavimo dviejų realiųjų skaičių pora, jį pavaizduojame kompleksiniu skaičiumi. Nauda akimirksniu!
Kodėl? Nes kompleksiniams skaičiams mes turime poliarinę formą ir puikų jų sąryšį su kampais. Štai, kai dauginate du kompleksinius skaičius, dauginate jų dydžius (absoliutines vertes) ir sudedate jų poliarinius kampus (argumentus). Veiksmai su kampais ir sukiniais tampa visai paprastais.
Panagrinėkime tokį pavyzdį. Tarkim, reikia rasti kampų a, b ir
g sumą.
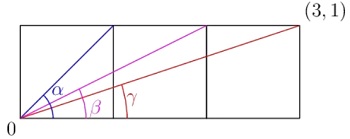
Atsakymas labai paprastas. Tie kampai atitinka kompleksinius skaičius 1+i, 2+i ir 3+i. Norint rasti tų kampų sumą, tereikia sudauginti tuos skaičius. Gauname:
(1+i)(2+i)(3+i)=10i
Kas reiškia, kad turime stačią kampą (90o)!
Pereikime istoriją. Atradus esant iracionalius skaičius, atsirado ir tai neigiantys. Įvedus arabišką skaičiavimo sistemą, buvo jos nepriimančiųjų. Buvo murmančiųjų po kalendoriaus reformos. Atsiradus mašinoms, išstojo luditai. Prieš kontracepciją stoja krikščionys. Taip buvo ir su neigiamais ir menamais skaičiais, aibių teorija, ne-euklidine geometrija, pirmosiomis spausdinimo mašinėlėmis, skaičiavimo metodų matematika, funkciniu programavimu...
Tačiau tokiomis prieštaromis pasaulis nėra užpildytas ir tik laiko klausimas, kada prasimuš naujos idėjos ir technologijos. Senosios kartos, kaip ir tokios užgaidos kaip C, Lisp, Perl išmirs. Neišvengiamai - tai tik laiko klausimas. Progreso pagrindas yra mokslas. Visų mokslų varomoji jėga yra matematika. Bet yra skirtumas tarp mokslo ir paramokslo. Scientologijos bažnyčia yra tas antrasis.
Apie racionalius skaičius ši kalba
Sveiki skaičiai, trupmenos (tiek teigiami, tiek neigiami) ir nulis sudaro racionalių skaičių aibę. Bet kurį racionalų skaičių galime laikyti trupmena m/n, kai n nelygu 0 (pvz., -5=-5/1).
Racionalius skaičius galima išreikšti begalinėmis periodinėmis dešimtainėmis trupmenomis,
pvz., 2/5=0,4000...; -9/7=-1,285714285714285714
.=1,(285714)
Teisingas ir atvirkščias teiginys: bet kurią dešimtainę periodinę trupmeną galime išreikšti paprasta trupmena, pvz.
0,3666
=(36-3)/90=33/90=11/30
Plačiau apie tai >>>>>>
Atlikdami aritmetikos veiksmus (sudėtį, atimtį, daugybą ir dalybą) su racionaliais skaičiais rezultate gauname irgi
racionalų skaičių, t.y. šie veiksmai mus palieka racionalių skaičių aibėje.
Taigi ji yra adityvinė grupė su nuliniu elementu 0, kurioje
atvirkštiniai skaičiai yra neigiami. Ji žymima Q, o
gretinių (ar kortežų, angl. tuples) notacija (Q,+,0,-), o taip pat ji yra ir laukas.
Tai galioja ir pirmos eilės lygtims su vienu nežinomuoju bei pirmos eilės lygčių sistemoms su keliais nežinomaisiais jei jų koeficientai ir laisvieji nariai yra racionalūs skaičiai, tai nežinomojo reikšmė taip pat racionalusis skaičius. Pvz. (3/2)x-5/2=0 išsprendžiama kaip x=5/3
Periodinės dešimtainės trupmenų vertimas paprastąja
Periodinę dešimtainę trupmeną a=0,3(15) išreiškime tokiu pavidalu:
b=0,3(15)=0,31151515... = 0,3+0,015+0,00015+0,0000015+
=0,3+15*10-3+15*10-
7+15*10-9+
Ji, pradedant antru nariu (po 0,3), yra mažėjanti geometrinė progresija, kurios pirmas narys yra a=0,015, su
daugikliu q=-2. Begalinės geometrinės progresijos narių suma yra lygi
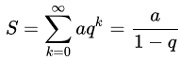
Tad jos reikšmė yra b=3/10+(15*10-3)/(1-10-2)=3/10+15/990=(315-3)/990=52/165
Taigi taisyklė mišriajai periodinei trupmenai būtų:
Trupmenos skaitiklyje iš skaičiaus iki antrojo periodo (pvz., 315) atimti skaičių iki pirmojo periodo (pvz, 3), o
vardiklyje skaitmenį 9 užrašyti tiek kartų, kiek skaitmenų yra periode, o tada 0 tiek kartų, kiek yra skaitmenų iki periodo.
Pvz., b=0,42(7)=0,427777 .=(427-42)/900=77/180
Grynąją periodinę trupmeną paversti dar paprasčiau, pvz., b=1,272727 =1+(27-0)/99=14/11
Pastaba: Tą taisyklę dar performuluosime kitaip, kad taptų dar aiškesnė:
Periodinė trupmena lygi paprastajai trupmenai, kurios skaitiklyje parašytas skaičius lygus tarp kablelio ir
antrojo periodo bei skaičiaus tarp kablelio ir pirmojo periodo skirtumui. Vardiklyje rašomas skaičius, turintis tiek
devynetų, kiek skaitmenų yra periode, ir pridedama tiek nulių, kiek skaitmenų yra tarp kablelio ir pirmojo periodo.
Iracionalumo sąvokos ištakos
Susipažinkite: Matematika Babilone

![]() iracionalumo nustatymas priskiriamas senovės graikams,
pitagoriečiams (apie 570-495 m. pr.m.e.;
Teodorui iš Kirenės). Bet gali būti, kad juos atrado Hipas, - ir tas atradimas kainavo jam gyvybę
(žr. >>>>>).
Tačiau indai 150-200 m. anksčiau galėjo būti nustatę kvadratinių šaknų iš 2 ir 21 iracionalumą.
iracionalumo nustatymas priskiriamas senovės graikams,
pitagoriečiams (apie 570-495 m. pr.m.e.;
Teodorui iš Kirenės). Bet gali būti, kad juos atrado Hipas, - ir tas atradimas kainavo jam gyvybę
(žr. >>>>>).
Tačiau indai 150-200 m. anksčiau galėjo būti nustatę kvadratinių šaknų iš 2 ir 21 iracionalumą.
2016 m. kovą amerikiečiai B.M. Altschuler'is ir E.L. Altschuler'is paskelbė tyrinėjimą, kad senovės
šumerų ir akadų žyniai turėjo metodus, ledžiančius spėti ![]() iracionalumą (aišku, tais laikais tokios sąvokos nebuvo, ir svetainės, teigiančios, kad jie tai įrodė, skelbia nonsensą).
iracionalumą (aišku, tais laikais tokios sąvokos nebuvo, ir svetainės, teigiančios, kad jie tai įrodė, skelbia nonsensą).
Jiedu išnagrinėjo YBC 7289 ir BM 15285 molines lenteles, pateikiančias apytikslį ![]() skaičiavimą: pirmoji leidžia paskaičiuoti reikšmę iki 6-o ženklo po kablelio (skaičiuojant kvadrato
įstrižainę), o antroji turi savyje geometrinį reikšmės iracionalumo įrodymą bei geometrinį Pitagoro teoremos įrodymą.
skaičiavimą: pirmoji leidžia paskaičiuoti reikšmę iki 6-o ženklo po kablelio (skaičiuojant kvadrato
įstrižainę), o antroji turi savyje geometrinį reikšmės iracionalumo įrodymą bei geometrinį Pitagoro teoremos įrodymą.
Graikų ![]() iracionalumo įrodymas buvo algebrinis
ir rėmėsi prieštara: tarus, kad
iracionalumo įrodymas buvo algebrinis
ir rėmėsi prieštara: tarus, kad ![]() yra racionalus skaičius p/q, kur p ir q yra tokie, kad trupmena nesusiprastina. Paprastais veiksmais parodoma, kad p ir q
yra lyginiai, o tai prieštarauja mūsų prielaidai. Po šimtmečio Teodoras iš Kirenės (5 a. pr.m.e.) jau
mokėjo įrodyti kvadratinės šaknies iš 3, 5 ir kitų skaičių iki 17 iracionalumą.
yra racionalus skaičius p/q, kur p ir q yra tokie, kad trupmena nesusiprastina. Paprastais veiksmais parodoma, kad p ir q
yra lyginiai, o tai prieštarauja mūsų prielaidai. Po šimtmečio Teodoras iš Kirenės (5 a. pr.m.e.) jau
mokėjo įrodyti kvadratinės šaknies iš 3, 5 ir kitų skaičių iki 17 iracionalumą.
Pavyzdys
Teiginys. Lygtis x2=3 neturi racionalių šaknų.
Įrodymas.
Tarkim priešingai, kad x=m/n, kur m/n yra nesupaprastinama trupmena. Tada
x2=(m/n)2=3, kas neįmanoma, nes nesuprastinamos trupmenos kvadratas irgi yra nesuprastinama trupmena,
todėl ji negali būti lygi sveikam skaičiui. Tad lygties x2=3 sprendinys negali būti racionaliuoju skaičiumi.
Klausimas. Kokia yra dviejų iracionalių skaičių suma ar skirtumas iracionali ar racionali?
Atsakymas. Iš tikro, gali būti bet kokia. Ji gali būti ir racionali, pvz., p ir (5-p) yra iracionalūs skaičiai, tačiau jų suma p+(5-p)=5 yra racionali.
Pvz., įrodyta, kad e ir p yra iracionalūs (ir net transcendentalūs) skaičiai. Bet kokie yra e+p, e-p, ep, e/p, pe? Tai nėra nustatyta... Nežinoma, ar jie racionalūs, iracionalūs ar transcendentiniai. Tačiau iš to, kad e ir p yra transcendentalūs, seka, kad (x-p)(x-e)=x2-(e+p)x+ep negali turėti racionalių koeficientų. Tad (e+p) arba ep (arba abu) yra iracionalus.
Išspręstas iracionaliųjų skaičių aproksimavimo klausimas
Paprastai iracionalieji skaičiai aproksimuojami dešimtaine reikšme ar trupmena. Pvz., p reikšmė nurodoma kaip 3,14..., 157/50 arba 22/7 (ir pan.). Bet tada kyla klausimas: ar yra riba tų aproksimacijų paprastumui ir tikslumui? Ir ar galime pasirinkti bet kokios norimos formos trupmeną?
1941 m. fizikas R. Dufinas ir matematikas A. Schaefferis pasiūlė paprastą taisyklę atsakymams į tuos klausimus. Pirma, reikia apsispręsti, kiek tiksli turi būti trupmenos aproksimacija pasirinktam skaičiui vardiklyje. Aišku, kuo didesnis vardiklis, tuo mažesnė klaidos tikimybė. Jei pasirinkta paklaida yra labai maža, tada yra tik ribotas skaičius vardiklių, užtikrinančių gerą aproksimaciją. Jei paklaida gana didelė, tada aproksimacijų yra gana daug ir didindami vardiklį galime gauti bet kokį norimą tikslumą.
Tačiau esmė ta, kad arba galite aproksimuoti bet kurį laisvai pasirinktą iracionalų skaičių, arba jokio. Tai pribloškianti dichotomija. Ir nors atrodytų logiška, kad mažesnėms klaidoms sunkiau aproksimuoti, R. Dufinas ir matematikas A. Schaefferis neįstengė to įrodyti. Ir tik 2019 m. vasarą Oksfordo un-to prof. D. Koukoulopoulos su kolega J. Maynardu paskelbė apie savo įrodymą.
Jie pasinaudojo grafų teorija, leidusia naujai vizualizuoti uždavinį. Tai daugelį matematikų nustebino ir gali būti, kad ateityje grafai bus plačiau naudojami įrodymuose. Tiesa, gali praeiti net keli mėnesiai, kol bus pilnai suprastos visos 44 psl. įrodymo detalės ten daug dalykų dar reikalauja kruopštaus patikrinimo.
Skaičiai kitaip
Yra daug būdų pateikti skaičiais. Mums įprastoje dešimtainėje sistemoje sveiki skaičiai yra sudaromi taip: a+bx+cx+ , t.y., pvz., 3725=5+2*10+7*100+3*1000. Kitaip sakant, ši schema paremta sudėtimi. Sveiki skaičiai a, b, c, yra iš skaitmenų {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} aibės ir bet kuris teigiamas sveikas skaičius yra išreiškiamas unikaliai tokiu būdu. Yra ir kitų išraiškos būdų. Kompiuterių pasaulyje plačiai naudojamas dvejetainis pagrindas, kai skaičius išreiškiamas 0 ir 1 seka, pvz., 73=1001001
Tačiau čia pabandysime kitą skaičiaus atvaizdavimo dešimtainėje sistemoje būdą, paremtą ne sudėtimi, o atimtimi, kurią įkvėpė Nigerijos jorubių tauta, kurios atstovas 15 apibrėžtų kaip 5 iki 20, 16 kaip 4 iki 20 ir t.t. iki 19 kaip 1 iki 20.
Tokia prieiga prie skaičių nėra visiškai unikali panašiai yra ir su romėniškais skaičiais, kur 4 vaizduojama kaip IV, 9 kaip IX, 90 kaip XC ir pan. Net mes kartais laiką nurodome maždaug taip penkiolika iki pirmos, kai norime pasakyti, kad yra 12:45.
Pabandysime apibendrinti jorubių naudojamą sistemą. Tik neatsižvelgsime, kad iš tikro jorubiai sistemos pagrindui naudoja 20 ir minėto būdo netaiko skaičiams iki 15.
Taigi, 15 naujoje sistemoje užrašykime kaip 25, kur 5 reiškia minus 5, t.y. 25=2*10-5. Naujoje sistemoje
vietoje mūsiškės N naudojama tokia žymenų aibė: N = {0, 1, 2, 3, 4, 5, 4, 3, 2, 1}. Joje galime išreikšti
bet kurį skaičių, pvz., minėtas 3725=4335=(40-3)*100+30-5
Tokį skaičių pateikimo būdą pristatėme visai kaip įdomią teorinę, o ne praktinę (ir siūlymą jį naudoti) galimybę,
nors jos principai sutinkami ir kitur (romėniškuose skaičiuose, laiko nurodyme,
).
Nustatom Visatos struktūrą
Amerikiečių fizikas F. Benfordas sakė: Skaičiai tėra tik blyškūs realiai egzistuojančių daiktų simboliai.
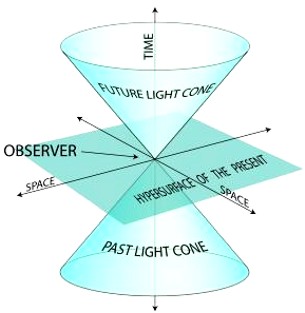
Einšteino erdvėlaikyje atstumas matuojamas realiaisiais skaičiais, o laikas menamais skaičiais. Taigi specialiosios reliatyvumo teorijos erdvėlaikis yra Minkovskio erdvė. Stebėtojas erdvėlaikyje brėžia pasaulio liniją praeities ir ateities įvykių kūgiuose (šviesos kūgiuose). Srityse už tų kūgių vykstantys įvykiai mums pasiekiami tik didesniais už šviesą greičiais.
Šių kūgių pjūvių plokštumomis kreivės yra hiperbolės, tad matematika erdvėlaikyje yra hiperbolinė, o ne įprastinė trigonometrinė (apskritiminė).
Šviesos kūgis - tai hiperpaviršius erdvėlaikyje (dažniausiai Minkovskio erdvėje), ribojantis tam tikro įvykio praeities ir ateities sritis. Jis suformuojamas erdvėlaikyje izotropiniais vektoriais, t.y nenuliniais nulinio ilgio vektoriais. Jį galima suprasti kaip visų taškų aibę, kuriems intervalas, skiriantis nuo įvykio (šviesos kūgio viršūnės) yra pasiekiamas šviesos greičio (t.y. lygus nuliui). Šviesos kūgio ašis sutampa su nejudančios duotoje atskaitos sistemoje dalelės pasaulio linija. Šviesos kūgis erdvę padalija į tris sritis priežasties-pasekmės sąryšio prasme: praeities, ateities ir absoliučiai nutolusią (kurioje įvykis neturi priežastinių-pasekminių ryšių).
Pasaulio linija - objekto kelias erdvėlaikyje (besiskirantis nuo orbitos ar trajektorijos), įtraukiantis judėjimą laike. Jos sąvoka pirmąkart kilo H. Minkovskiui ir yra svarbi teorinėje fizikoje. Tai erdvinių-laikinių įvykių seka (kreivė) atitinkanti objekto istoriją. Kiekvienas jos taškas tai įvykis, kurį galima pažymėti laike ir padėtimi erdvėje. Dvi susikertančios pasaulio linijos reiškia susidūrimą. Dvi linijos prasidedančios viename taške reiškia du galimus istorijos vystymosi kelius (arba dalelės skilimą į dvi).
Kiek apvaliau skaičių apvalinimas
![]() Visi žino apie skaičių apvalinimą. Jei batų kaina parduotuvėje nurodyta 99.99 Lt, jūs žinote, kad iš tikro už juos mokate 100 lt.
Visi žino apie skaičių apvalinimą. Jei batų kaina parduotuvėje nurodyta 99.99 Lt, jūs žinote, kad iš tikro už juos mokate 100 lt.
O kvantinėje mechanikoje galimos tik tam tikros reikšmės. Tai kažkiek primena kiaušinių pirkimą. Paprastai perkame po 10 arba 5 kiaušinius, tačiau niekada neperkam pusės kiaušinio.
Taip ir kompiuteriai saugo informaciją kaip bitų (dvejetainių skaičių, 0 ir 1) sekas. Atvaizduodami vaizdus monitoriuje, jie perteikiami taškais (pikseliais). Nebus pavaizduota tai, kas yra tarp dviejų pikselių. Kompiuteris turi tai suapvalinti iki kurio nors pikselio. O tada kartais dėl apvalinimo paklaidos mažyčiai apskritimai tampa labiau panašūs į mažus kvadračiukus.
Ir kadangi mes gyvename kvantiniame pasaulyje, jame irgi neišvengiamos apvalinimo paklaidos. Kvantiniame tunelyje šios paklaidos gali sumuotis ir tada objektai gali judėti didesniu už šviesą greičiu. Panašūs dalykai pastebimi spartesniuose už šviesą peršokimuose, kurie leidžia medžiagai palikti juodąsias skyles, arba elektronams pereinant į dielektrinę terpę.
Skaičių grupavimas vektoriai, matricos ir tenzoriai
Vektorius yra atstumas su kryptimi. Matrica yra vektorių rinkinys. Tenzorius yra vektorius su sukinio reikšme.
Atradę kompleksinius skaičius, galime įvesti skaičių rinkinius, suprantamus kaip atskiras reikšmes. Taip galime įsivaizduoti koordinates, aibes arba skaičių tinklelius kaip atskirus skaičius. Pvz., padėtį erdvėje galime nurodyti kaip (3, -7, 2), kad gali reikšti: paeiti į šiaurę 3 m, tada į vakarus 7 m ir pakilti į viršų 2 m.
Taip pat (3, -7, 2) gali atvaizduoti traukimo jėgą. Jus virve 3 žmonės tempia į šiaurę, 7 - kita virve tempia į vakarus, 2 - trečia virve tempia aukštyn. Tai gali būti jėgos vektoriaus pavyzdys. Papildykime jį papildomais skaičiais apibūdinančiais vektoriaus sukinį ir turėsime jėgos tenzorių - o tai būtų matrica iš dviejų vektorių (dviejų eilučių arba stulpelių).
Dar nelabai aišku? Pateikiame paaiškinimą ant pirštų...
Tenzoriaus samprata
Pabandysime paaiškinti tenzoriaus savoką, nesileisdami į dideles matematines vingrybes ir nesilaikydami matematinio griežtumo.
Pradžioje apie termino tenzorius reikšmę ir teorijos kilmę. Jis kilęs iš anglų kalbos žodžio tension (tempimas) ir pirmąkart V. Hamiltono panaudotas 1846 m., tačiau jis reiškė visai kitką, nei dabartinėje matematikoje ir matematinėje fizikoje. Dabartine prasme terminą įvedė V. Voigtas, o tenzorinį skaičiavimą maždaug 1890 m. įvedė G. Riči. 20 a. jis išpopuliarėjo po panaudojimo Einšteino bendrojoje reliatyvumo teorijoje po 1915 m.
Terminas kilo apmąstant tokį uždavinį. Tarkim, kad trimatėje erdvėje turime neapibrėžtos
formos kietą kūną, kurį skirtinguose jo taškuose veikia įvairios jėgos. Kaip aprašyti kylančius
tempimus kokiame nors to kūno pjūvyje?
Atsakymas tempimas aprašomas tenzoriniu lauku.
Bet pradžioje peržiūrėkime paprastesnius atvejus.
Paimkime vienalytį kubą ir pakaitinkime jį iš kurios nors vienos pusės. Tada pasirinktu laiko
momentu pabandykime aprašyti temperatūrą kiekviename kubo taške. Temperatūra yra
skaliarinis skaičius, mes turime tik vieną reikšmę.
Įsiveskime bet kokią koordinačių sistemą. Joje temperatūra bus aprašyta kaip skaliarinė funkcija su parametrais (x,y,z).
Tada paimkime kitą koordinačių sistemą ir pažiūrėkime, kas pasikeitė. Ogi nieko. Temperatūra
kiekviename taške liko tokia pati! Taigi gavome matematinį objektą, skaliarą, kuris nesikeičia
pakeitus koordinačių sistemą. Pavadinkime jį nulinio laipsnio tenzoriumi.
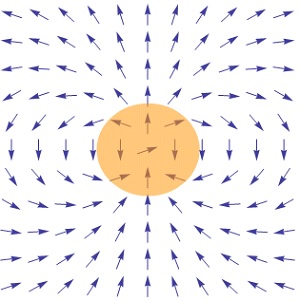
Pakaitinus mūsų kūną, jame molekulės ėmė kažkaip judėti. Vėl paimkime kokį nors laiko momentą
ir pabandykime aprašyti molekulių judėjimą kiekviename kubo taške.
Greitis tai vektorius (molekulė juda tam tikru geičiu tam tikra kryptimi), tad molekulių
greičiai bus aprašyti kaip vektorinės funkcijos su parametrais (x,y,z).<
Vėl paimkime kitą koordinačių sistemą. Vektorinis greičių laukas kube nepasikeitė mes tiesiog
paėmėme kitą liniuotę (t.y. koordinačių sistemą) greičių matavimui. Žinodami ankstesnę ir naują
koordinačių sistemas, galime išvesti vektoriaus reikšmių pasikeitimo funkciją.
Taigi gavome matematinį objektą, vektorių, kuris vėlgi nesikeičia keičiant koordinačių sistemą. Tai pirmojo laipsnio tenzoriumi.
Galim panašiai eiti ir toliau. Viską darykime taip pat, tik tegu mūsų kubas nėra vienalytis,
jame viduje yra įvairių priemaišų, ertmių, tad kaitinant kubą, molekulių greičiai skirtingose
vietose ima skirtis. Kaip aprašyti tokią nevienalytę terpę?
Vėl fiksuokime tam tikrą laiko momentą ir paimkime vieną molekulę su jos greičio vektoriumi.
Paklauskime, kaip šis vektorius pasikeis kitu laiko momentu? Tai labai panašu į tai, kad
kiekviename kubo taške yra kažkas, kas moka pasukti vektorių ir pakeisti jo ilgį. O taip tai juk
matrica, tačiau speciali, tokia, kuri nesunaikina vektoriaus, o tik jį transformuoja.
Kas nutiks mūsų matricai, jei pakeisime koordinačių sistemą? Kubo vidinė sandara liko tokia pat,
tad matrica turi sukioti vektorius lygiai taip pat. Na taip, matricos reikšmės pasikeitę, tačiau jos poveikis vektoriui liko toks pat.
Tad vėl, gavome matematinį objektą, specialaus pavidalo matricą, kurios poveikis
vektoriui nesikeičia keičiant koordinačių sistemą. Tai antrojo laipsnio tenzorius.
Taigi, kas yra tas tenzorius? Tai matematinis objektas, pats savaime nepriklausantis nuo koordinačių sistemos kaitaliojimo, tačiau jo komponentės kinta pagal nustatytą matematinį dėsnį. Trimatėje erdvėje antro laipsnio tenzorių galima įsivaizduoti kaip matricą kiekviename erdvės taške, aprašančią tos erdvės nevienalytiškumą ir veikiančią įeinantį į tašką vektorių, keičiant jo kryptį ir ilgį. Analogiškai, galima tęsti toliau, įvedant 3, 4, 5, laipsnių tenzorius.
Taigi, tikiuosi, intuityviai supratote, kas yra tenzorius, teliko išaiškinti naudojamą matematinę notaciją (žymenis), bei aprašyti veiksmus su tenzoriais. Bet tai planuojam atskirame puslapyje...
Susiję terminai
|
1. Pseudo-euklidinė metrika Minkovskio erdvėje, apibrėžiama 2. Visų vektorių su nuliniu intervalo kvadratu aibė suformuoja kūgio paviršių ir vadinama šviesos kūgiu. 3. Vektorius, esantis šviesos kūgio viduje, vadinamas panašiu į laiką vektoriumi; jo išorėje - panašiu į erdvę. 4. Įvykis duotuoju laiko momentu duotame taške vadinamas pasaulio tašku. 5. Pasaulio taškų aibė, aprašantys (materialios) dalelės judėjimą laike, vadinama pasaulio linija. 6. Inercinis stebėtojas - tas, kuris randasi ar juda tiesiai ir tolygiai (nesisukant jo koordinačių
sistemai) inercinės atskaitos sistemos atžvilgiu. Lorenco (Galilėjaus) koordinatėse tokio stebėtojo pasaulio
linija (ir visų taškų, nejudančių jo atskaitos sistemoje) atrodo labai paprastai: 7. Intervalas tarp dviejų įvykių, per kuriuos pereina stebėtojo pasaulio linija, padalintas iš c, vadinamas jo savu laiku, nes tas dydis sutampa su laiku, matuojamu kartu su stebėtoju judančiu laikrodžiu. Neinerciniam stebėtojui savas laikas tarp dviejų įvykių atitinka intervalo pasaulio linija integralui. |
Minkovskio erdvė
Minkovskio erdvė - 4-matė pseudo-euklidinė erdvė, pasiūlyta kaip erdvėlaikio specialiojoje reliatyvumo teorijoje geometrinė interpretacija. Ji pavadinta matematiko Hermano Minkovskio vardu.
Atstumas tarp dviejų įvykių Minkovskio erdvėje yra:
- erdvinis;
- šviesinis (nulinis);
- laikinis.
Kiekvieną įvykį atitinka Minkovskio erdvės taškas Lorenco (arba Galilėjaus) koordinatėse, kurio trys koordinatės yra trimatės euklidinės erdvės Dekarto koordinatės, o ketvirtoji perteikia ct koordinatę (c - šviesos greitis; t - įvykio laikas). Todėl, kai simetrinė grupė euklidinėje erdvėje yra euklidinė grupė, simetrinė grupė Minkovskio erdvėje yra Puankarė grupė.
1906 m. A. Puankarė
pastebėjo, kad paėmus laiką kaip menamą ketvirtojo erdvėlaikio koordinatės
matavimo dalį ( ![]() ct),
Lorenco transformaciją galima suprasti kaip koordinačių pasisukimą 4-matėje
euklidinėje erdvėje su trimis realiosiomis erdvės koordinatėmis ir viena menama laiko koordinate. Kadangi
tada erdvė tampa pseudo-euklidine, pasukimas yra hiperbolinio pasukimo atvejis. Tačiau tos išvados A.
Puankarė nepadarė, nes jo tikslu tebuvo Lorenco transformacijos paaiškinimas per įprastinio euklidinio
pasukimo terminais. Tą idėją 1908 m. išvystė Hermanas Minkovskis, panaudojęs ją Maksvelo lygčių
performulavimui 4-iems matavimams, parodydamas jų invariantiškumą Lorenco transformacijos atveju. Vėliau jis performulavo Einšteino
specialiąją reliatyvumo teoriją. Iš to jis padarė išvadą, kad erdvė ir laikas
turi būti traktuojami vienodai, ir iš to kilo jo įvykių unifikuotame 4-mačiame erdvėlaikio kontinuume koncepcija.
ct),
Lorenco transformaciją galima suprasti kaip koordinačių pasisukimą 4-matėje
euklidinėje erdvėje su trimis realiosiomis erdvės koordinatėmis ir viena menama laiko koordinate. Kadangi
tada erdvė tampa pseudo-euklidine, pasukimas yra hiperbolinio pasukimo atvejis. Tačiau tos išvados A.
Puankarė nepadarė, nes jo tikslu tebuvo Lorenco transformacijos paaiškinimas per įprastinio euklidinio
pasukimo terminais. Tą idėją 1908 m. išvystė Hermanas Minkovskis, panaudojęs ją Maksvelo lygčių
performulavimui 4-iems matavimams, parodydamas jų invariantiškumą Lorenco transformacijos atveju. Vėliau jis performulavo Einšteino
specialiąją reliatyvumo teoriją. Iš to jis padarė išvadą, kad erdvė ir laikas
turi būti traktuojami vienodai, ir iš to kilo jo įvykių unifikuotame 4-mačiame erdvėlaikio kontinuume koncepcija.
*) Žanas Roberas Arganas (Jean-Robert Argand, 1768-1822) šveicarų kilmės prancūzų matematikas savamokslis. 1806 m., turėdamas knygyną Paryžiuje, išleido esė, kurioje iškėlė kompleksinių skaičių geometrinio atvaizdavimo mintį. Dabar tai vadinama Argano diagrama. O vėliau (1814) jis įvedė ir terminą kompleksinio skaičiaus modulis, t.y. atstumą iki koordinačių pradžios (0, 0). Tame pačiame darbe jis pateikė ir pirmą griežtą bei pilną Pagrindinės algebros teoremos rodymą.
Dalyba iš nulio
Pirminiai skaičiai
Kvadratinė lygtis
Aritmetikos pagrindai
Plotinas. Apie skaičius
Kokiu greičiu skriejame?
Ar įrodytas abc teiginys?
Nauja pirminių skaičių klasė
Kiek iš viso turime skaičių?
Nepaprasti Visatos skaičiai: 8
Kas tie romėniški skaitmenys?
Proveržis skaičiuojant skaidinius
Galilėjus, Dievas ir Matematika
Kirmgrauža tarp matematikos sričių
Aukso gysla Ramanadžano lygtims
Kita skaičiavimo metodų istorijos pusė
B.Raselas. Matematiko košmariškas sapnas
Pitagoro skaičiai per Fibonačio seką
Omaras Chajamas: ne vien Rubijatai
Skaičiai B ir jų kvantinės sistemos
Truputis apie skaičių psichologiją
Matematikos atgimimas Lietuvoje
Nepaprasti skaičiai: skaičius 42
Pagrindinės statistinės sąvokos
Nepaprasti Visatos skaičiai
Iniciatyva: Matematikos keliu
Didžiausias bendras daliklis
Didžioji Ferma teorema
Laplasas. Dėl tikimybių
Matematiniai anekdotai
Pitagoro teorema
Černo medalis
Nulio istorija
Vartiklis