Intuicijos ribojimas matematikoje 19-me amžiuje. Vartiklis

17 a. filosofinio racionalizmo atstovai Dekartas ir Leibnicas išvystė mokymą apie betarpišką, intuityvų pažinimą, remdamasis samprotavimais apie logišką patikimų tiesų – matematinės dedukcijos pagrindą sudarančių aksiomų – prigimtį. „Proto vadovavimo taisyklėse“ patikimos žinios laikomos pažinimu, kylančiu nuo intuityviai akivaizdžių teiginių ir išsirutuliojančiu į ilgas deduktyvių išvadų grandines. Ir nors kiekviena tos grandinės grandis pati savaime nėra intuityviai akivaizdus, tačiau visi perėjimai tarp grandžių pradedant pirminėmis aksiomomis yra intuityvūs aiškūs ir patikimi. Dekartas aiškino, kad intuicijos akivaizdumas ir patikimumas būtinas ne tik atskiriems teiginiams, bet ir įvairiems samprotavimams.

Imkim, pvz., teiginį „2 ir 2 sudaro tą pat, kaip ir 3 ir 1“. Jame būtina intuityviai suvokti ne tik tai, kad 2 ir 2 sudaro 4 bei ir 3 ir 1 sudaro 4, bet ir tai, kad iš šių dviejų teiginių būtinai seka tasai trečias. Ir nors daugelis mokslo tvirtinimų nėra savaime aiškiais, jie vis tik prieinami patikimam pažinimui, „jei tik jie išvedami iš patikimų ir suprantamų principų nuoseklaus ir nenutrūkstamo minties judėjimo būdu esant aiškiai intuicijai dėl kiekvieno atskiro teiginio“. Moters intuicija

Nemažiau svarbia matematikai bei kitoms patikimo pažinimo rūšims intuiciją laikė ir Leibnicas. Tiesa, jis aksiomas laikė įrodomomis ir todėl, kaip K. Gausas, deduktyvių mokslų pagrindais laikė apibrėžimus. Tačiau jie gali būti pradiniais principais tik todėl, jei yra intuityviai aiškūs ir patikimi: „Intuityvus pažinimas glūdi apibrėžimuose, kai jų galimumas iškart aiškus“. Ir toliau: visi adekvatūs apibrėžimai savyje turi pirmines racionalias tiesas ir „seka, intuityvias žinias“. Ir aplamai, jos (pirminės racionalios tiesos) betarpiškos idėjų betarpiškumu“. Vadinamasis demonstratyvusis pažinimas tėra „intuityvių pažinimų tarpinių idėjų sukabinimas visais ryšiais“. Todėl demonstratyvusis pažinimas, sustiprinant Dekarto mintį, kurią pakartojo ir Lokas, „ne toks aiškus kaip atvaizdas, kelių veidrodžių atspindėtas, vis labiau blunka su kiekvienu atspindžiu, ir jį jau ne taip lengva atpažinti“.

Bendru pagrindu jiedviem buvo dvi prielaidos: a) įsitikinimas, kad aksiomose (ar apibrėžimuose) santykis tarp loginio subjekto (S) ir predikato (P) yra besąlygiškai visuotinis ir būtinas santykis [19 a. matematikoje buvo įrodyta, kad tai klaidinga]; b) įsitikinimas, kad besąlyginis visuotinumo ir būtinumo pobūdis negali būti gautas nei iš jokios patirties, nei empirinės indukcijos, o tegali būti išmąstytas.

Leibnicui matematinė intuicija liko susijusi su matematinių įrodymų logika. Besąlygiškai privalomas aksiominio sprendimo S – P santykis yra ne tik mąstymo rezultatas arba intuicija, bet ir analitinės išvados santykis: predikatas P seka iš savo subjekto S, nes P turinys yra S turinio dalis ir todėl gali būti analitiškai išvestas iš S: S -> P.

Čia jau įžvelgiamas požiūris į matematiką kaip įrodomų teiginių sistemą. Juose intuityviu, t.y. betarpiškai suvokiamu, galima laikyti ne tiek turinį, kiek patį loginį perėjimą nuo ankstesnių teiginių prie išvestinių. Į pirmą planą iškyla visas dedukcines grandis siejančios loginės tapatybės santykio klausimas. Dedukcijos elementų turinio apmąstymas, buvęs svarbus antikos matematikams, netenka prasmės. Analitinė teorija rodė kelią į kažkokią labai bendrą logiką, griežtą dedukcinę sistemą.

Tad naujųjų laikų matematikai susidūrė dvejopa tendencija intuicijos supratime. Iš vienos pusės, intuityvūs, betarpiški santykiai tarp matematinių objektų kaip matematinio patikimumo pagrindas, o pačios intuicijos – kaip pirminiai „statybiniai“ elementai [Dekartas, Leibnicas]. Iš kitos – loginis matematikos pagrindimas [irgi Leibnicas: laiške Hiuigensui rašo: „Nustačiau kai kuriuos naujus simbolinės kalbos, besiskiriančius nuo algebros, pradus; jos dėka bus galima naudingiau, tiksliau ir arčiau reikalo, be figūrų, mintyse, pateikti visa, kas priklauso nuo intuicijos“].

Tačiau reikalai ta kryptimi pajudėjo ne iškart. Net Leibnico pasekėjo Ch. Volfo¹⁾ mokykloje analitinės matematikos sampratos iš esmės nebuvo. O tuo tarpu Vokietijoje atsirado mąstytojas, kurio mintys gerokai kirtosi su analitiniu matematikos mąstymu. Tai buvo I. Kantas.

Jis atmetė racionalistų intelektualiąją intuiciją, kas nulėmė I. Kanto gnoseologinis agnosticizmas, t.y. proto nesugebėjimas pažinti daiktus tokiais, kokie egzistuoja patys savaime. Kantas nusprendė, kad Leibnico intelektualizmas negali paaiškinti matematinio pažinimo prigimties. Jis išsaugojo įsitikinimą, kad matematika apima neabejotinai visuotines tiesas ir tas visuotinumas negali kilti iš patirties. Tačiau tų apriorinių tiesų šaltinis ne išprotavimai, o aprioriniai suvokimai. Geometrijos ir aritmetikos aksiomos – aprioriniai sprendimai, besiremiantys intuicija, kurios pagrindas juslinis.

Aptarimas „Kas yra matematika?“ filosofijoje aptarima jau nuo seno – pradedant Platonu ir Aristoteliu, o baigiant neoplatoniku Proklu, kuris laikė, kad matematika yra ant ribos tarp tikro apmąstymo, leidžiančio pažinti be ribų ir vaizdinių, ir juslinio suvokimo. Matematikoje mintis sudaiktėdama iškyla kaip racionalus darinys, o juslinis suvokimas apsivalydamas virsta matematine „įsivaizduojama medžiaga“. Taigi, pagal Proklą matematikos prigimtis dvilypė: ji yra kompromisas tarp gryno mąstymo ir gryno juslingumo: „gebantis racionalioms konstrukcijoms, tačiau nepajėgiantis jų nagrinėti kaip sudėtingų darinių, skaido į paprastesnius komponentus ir perveda į kitą nagrinėjimo sritį – perduoda juos vaizduotei ir jau joje, arba su jos pagalba, pateikia apie juos išsamias žinias“. Toliau sekė R. Dekarto „gryno suvokimo“ ir vaizduotės išskyrimas bei G. Leibnico idėja apie matematinį pažinimą, gaunamą iš dviejų sugebėjimų: vaizduotės ir proto.

Ir jei Proklas aiškiai neišskyrė įsivaizduojamo juslinio objekto (pvz., kentauro) ir įsivaizduojamo matematinio objekto, tai tą trūkumą pašalino I. Kantas, nurodęs, kad geometrijoje nagrinėjami objektai nėra empiriniai (t.y., nebūtina, pvz., brėžti begalinę tiesę, kad įsitikintume, kad ji nesikerta su lygiagrečia jai – pakanka nurodyti atitinkamos figūros sukonstravimo būdą). Ir objektus, sukurtus gryno apmąstymo būdu, nepriklausomai nuo galimybės juos sukonstruoti empiriškai, I. Kantas taip pat pavadina a priori.
Dar žr. >>>>>

Ir vis tik I. Kanto matematikos teorija buvo neaiški ir pilna prieštaravimų, tad ją skirtingos 19 a. pab. - 20 a. pr. kryptys priėmė labai skirtingai. Amžių sandūroje pasirodė prancūzo Liuji Kutiuro ir anglo Bertrano Raselo tyrinėjimai, skirti Leibnico logikai.

19 a. matematikos vystymasis parodė, kad antikos mokslo dedukcijose nebuvo pakankamo griežtumo. Tai buvo dėl pasitikėjimo vaizdžiu pateikimu (pvz., Euklidas, įrodinėdamas trikampių kongruentumą, remiasi tuo, kad trikampį galima perkelti ir uždėti ant kito trikampio). Ypač tai iškalbinga senovės Indijos matematikoje – kiekvienai teoremai sudarydavo brėžinį ir vietoje įrodymo parašydavo: „žiūrėk“. Net naujųjų laikų Fojerbachui suvokimo betarpiškumas atrodė idealu: „Naujoji filosofija siekė kažko betarpiškai patikima. [ … ] Teisinga tik tai, kam nereikia jokio įrodymo, kas betarpiškai teisinga savaime, kas betarpiškai kalba už save […], kas yra vienareikšmiškai apibrėžta ir neabejotina, suprantama, kaip saulė danguje“. Taigi, Fojerbachas neigė Hėgelio tezę, kad viskas tarpiška. Ir net Leibnicas laikė, kad „būtų beprotybe reikalauti kiekvieno dalyko įrodymo ir nesivadovauti aiškiomis ir akivaizdžiomis tiesomis“.

Tačiau Leibnicas jau suvokė, kad matematikoje intuityvus akivaizdumas jau nėra pagrindas atsisakyti griežtų įrodymų tiesoms, atrodančioms aiškioms ir akivaizdžioms. Neįrodomos tik „pirminės“ arba „betarpiškos“ aksiomos; tuo tarpu „antrinės aksiomos“ turėtų būti įrodomos.

Tačiau tokios sampratos kelias nebuvo lengvas. B. Raselas straipsnyje „Naujausi darbai apie matematikos pagrindus“ (1901 m. liepa) parodė, kad intuityvus akivaizdumas kartais gali suklaidinti. Taigi įrodymas visai ne tuščias ir bereikalingas užsiėmimas. Ir net įrodinėdama akivaizdžius dalykus, matematika tuo pačiu atskleidžia „tikrai naujas tiesas“.

Matematinės analizės ir geometrijos vystymasis reikalavo griežto pagrindimo. Tai padarė 19 a. didieji matematikai, pradedant Gausu bei Koši, ir baigiant Vejerštrasu²⁾. Mažėjo intuicijos svarba. Pasirodė, kad dalis teiginių, priimtų remiantis intuicija, pasirodė esą klaidingi.

Lemiamu intuicijos nuvainikavimu buvo lygiagrečiųjų tiesių teorijos išvystymas bei kvaternionų atradimas. Iš Euklido pateikto lygiagrečių tiesių apibrėžimo „Dvi tiesės erdvėje vadinamos lygiagrečiomis, jei jos yra vienoje plokštumoje ir, pratęstos į begalybę, nesusikerta“ sekė 5-sis jo postulatas: „Jei tiesė, kertanti kitas dvi, sudaro vidinius taškus, kurių suma mažesnė už du stačius kampus, tai tiesės kertasi toje pusėje, kur vidinių kampų suma mažesnė už du stačius kampus“. Iš apibrėžimo ir šio postulato matosi, kad per tašką, esantį greta tiesės, galima nubrėžti tik vieną tiesę, lygiagrečią duotajai.

Iš vienos pusės, postulatas rėmėsi intuityviu aiškumu. Iš kitos pusės, apibrėžimas nusakė požymį, kurį galima patikrinti tik pratęsus tieses į begalybę. Tai jau nebuvo intuityvu. O kadangi graikų sąmonei buvo svetima begalybės sąvoka, dar antikos laikais imta ieškoti įrodymų 5-jam postulatui. Tie ieškojimai parodė, kad intuityvumo nepakanka geometrijos (ir aplamai, matematikos) pagrindimui.

19-e amžiuje pagausėjo analitiškai įrodytų teiginių, kurie atrodė prieštaraują intuityviam suvokimui, pvz., tolydžių funkcijų neturinčių išvestinių (kas geometrijoje atitinka netrūkias kreives, neturinčias liečiamųjų) atradimas ir kt. Pvz., Vejerštrasas pateikta formulė
Weierstrass function

kur a – laisvai pasirinktas nelyginis skaičius, o b – teigiamas, mažesnis už 1, skaičius. Ši funkcinė eilutė ribojama konvertuojančia eilute

, todėl funkcija w yra apibrėžta ir tolydi visiems x. Tačiau ši funkcija neturi išvestinių, bent jau esant

Mat bet kuriame kiek norime trumpame intervale, funkcija turi begalinė skaičių be galo mažų svyravimų. Tačiau matematika, apibrėžimų ir analizės veiksmų pagalba gali tirti ir tokių funkcijų savybes.
Apie Vejerštraso funkciją placiau skaitykite Monstriška funkcija

Tolimesniu svarbiu veiksniu „logizuojant“ matematiką ir mažinant intuicijos indėlį joje buvo Kanto matematikos filosofijos kritika.

I. Kantas laikė, kad geometrijos teoremos įrodomos tik figūrų sukonstravimu intuityviai suvokiamoje erdvėje ir nubrėžiant pagalbines linijas (žr. >>>>>). Viskas remiasi intuicija, vaizdžiu pateikimu. Neokantizmas laikėsi šio požiūrio, pvz., L. Nelsonas⁴⁾ nesutiko, kad matematikos „aritmetizacijos“ tikslu yra „visiškas matematinės intuicijos išstūmimas ir jos pakeitimas loginiu formalizmu“. Jo teigimu, matematinis pažinimas turi nuostabią ir paslaptingą ypatybę: jo apodiktiškumas tarytum „neleidžia ieškoti pažinimo šaltinio empirikoje; iš kitos pusės, neeuklidinės geometrijos dėka žinom, kad, tikėtina, tasai šaltinis negali glūdėti logikoje“. To „paslaptingumo“ atskleidimui L. Nelsonas ir atsisuka į kantiškąją „grynąją“ erdvės ir laiko intuiciją.

L. Kutiuras Kanto požiūrį dėl geometrinių įrodymų per erdvinę intuiciją laiko klaidingu: negalima remtis figūrų savybėmis, nes neretai jos tik menamos ir pasitikėjimas jomis gali nuvesti į sofizmus. O „pagalbiniai dariniai“ tėra metaforos, paimtos iš praktikos – įrodymo metu nubrėžta figūra visada yra tam tikros patirties idealizacijos rezultatas ir jos savybės iš anksto apibrėžtos figūros definicija. Pasakymas „sujunkime taškus A ir B“ reiškia ne daugiau nei „taškai A ir B apibrėžia tiesę dėl paties tiesės apibrėžimo“. Anot Kutiuro, neįmanoma sudaryti jokios figūros, kurios savybės nebūtų iš anksto nustatytos moksle pripažintais apibrėžimais. Tačiau konstravimai ne visada būtini. Sudėtingi ir painūs įrodymai gali būti pakeisti paprastesniais. Ten, kur toks pakeitimas galimas, nereikia įvesti jokių pagalbinių linijų, nes remiamasi esminėmis figūros savybėmis. Nebūtina „matyti“, pakanka žinoti jų abipusius santykius ir pritaikyti tinkamas teoremas. Galiausiai, geometrinis įrodymas gali virsti vien formalia logine dedukcija.

Pasirodė, kad intuicija nepatikima ir nepakankama priemonė ir skaičių teorijoje. Pvz., ilgą laiką laikyta intuityviai aiškia aksioma, kas sveikasis skaičius didesnis už savo dalį. T.y., jei tam tikra objektų visuma {A} yra kitos jų visumos {B} dalimi, tai A turi mažiau elementų nei B. Tačiau intuicija apgauna, kai elementų kiekis begalinis. Kantoras paaiškino, kad tame „nėra jokio prieštaravimo“. Pvz., teigiamų lyginių skaičių visuma yra natūrinių skaičių visumos dalis, tačiau jų elementų kiekis vienodas (vienoda aibių galia).

Ir vis tik tasai „sukilimas“ prieš intuiciją pats pateko į aklavietę. Ne visi matematikos principai pasidavė grynai loginiam pagrindimui. Kartu su kantiškosios intuicijos kritika vystėsi kito tipo intuicijos aiškinimasis. Jau 1905 ir 1906 m. matematikų ir filosofų pasitarimuose Vienoje buvo pasiūlytos tezės apie intuicijos vietą matematikoje. A. Hofleris³⁾ nurodė dvilypą tos tendencijos pobūdį. Vėliau buvo pabandyta išspręsti tą iškeltą antinomiją... Tačiau apie tolimesnius įvykius – jau kitą kartą (Kantoro aibių teorija ir tikrosios begalybės intuicija)...

Monstriška funkcija, pakeitusi supratimą apie skaičiavimo metodus

Skaičiavimo metodai - galingas matematinis įrankis, - ir nors sukurtas dar 17 a., tačiau liko ant klibančių pamatų. Jų pagrindinės koncepcijos remiasi intuicija ir neformaliais argumentais, o ne griežtais ir tiksliais apibrėžimais.

Padėties taisymui iškilo dvi mokyklos. Prancūzų matematikams toliau labiau rūpėjo taikyti skaičiavimus fizikos problemoms spręsti – pvz., planetų trajektorijoms arba elektros srovių elgesio nagrinėjimui. Tačiau 19 a. vokiečių matematikai pradėjo viską griauti – jie ėmė ieškoti kontr-pavyzdžių, kurie paneigtų jau nusistovėjusias prielaidas, o vėliau juos panaudojo, kad skaičiavimo metodus padėtų ant stabilesnio ir patikimesnio pagrindo. y=x2 liestinė

Ir vienu iš tų matematikų buvo Karlas Vejerštrasas. Ir nors jis anksti parodė gabumus matematikai, tėvas jį spaudė studijuoti finansus ir administravimą, kad stotų į Prūsijos tarnybą. Jam buvo nuobodūs universitetiniai kursai, tad jis, kaip teigiama, didžiąją laiko dalį praleisdavo gerdamas ir fechtuodamasis. 19 a. 4-ojo dešimtm. pabaigoje, negavęs diplomo, jis tapo mokyklos mokytoju, vesdamas pamokas nuo matematikos ir fizikos iki dailyraščio ir gimnastikos. Profesionaliai matematika užsiėmė tik prieš savo 40-metį. Tačiau jis transformavo tą sritį, sukūręs matematinį monstrą.

Jis 1872-ais paskelbė funkciją, sukėlusią grėsmę viskam, ką matematikai manė žiną apie skaičiavimo metodus. Ją ypač priešiškai priėmė prancūzų minties gigantai; A. Puankarė netgi apkaltino funkciją kaip „pasityčiojimą iš sveiko proto“, o Š. Ermitas ją pavadino „apgailėtina blogybe“.

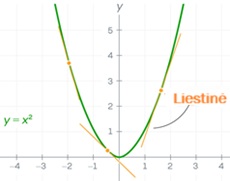
Bet norėdami suprasti tą reakciją, turime pradžioje panagrinėti dvi fundamentalias koncepcijas: tolydumą ir diferencijuojamumą. Tolydi funkcija (žr. tolydumo sąvokos vystymasis) – tai funkcija, neturinti trūkių ir šuolių. Ją galime įsivaizduoti kaip brėžiamą pieštuku, jo neatitraukiant nuo popieriaus. Skaičiavimo metodai daugiausia susiję su tokių funkcijų pokyčio greičio paskaičiavimu. Grubiai tariant, jie aproksimuoja tokią funkciją tiesiomis, nevertikaliomis linijomis.

Bet kuriame kreivės taške galima nubrėžti liestinę jai – tiesę, kuri geriausiai aproksimuoja kreivę šalia to taško. Liestinės nuolydis arba statumas rodo, kaip smarkiai funkcija keičiasi tame taške. Galite apibrėžti y=abs(x) grafikas ir kitą funkciją, vadinamą išvestine, kuri pateikia liestinės nuolydį kiekviename jūsų pradinės funkcijos taške. Jei išvestinė egzistuoja kiekviename taške, sakoma, kad pradinė funkcija yra diferencijuojama.

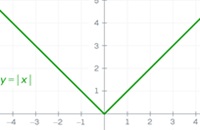
Funkcijos, kuriose yra trūkių, nėra diferencijuojamos. Tačiau net ir tolydžiosios funkcijos ne visada yra diferencijuojamos kiekviename taške. Paimkime absoliučios reikšmės (modulio), abs(x) arba y=|x|, funkciją, kurios grafikas atrodo taip (ir ji nėra diferencijuojama nuliniame taške):

Tai netrikdė daugumos 19 a. matematikų, kurie tai laikė pavieniu reiškiniu ir teigė, kad tol, kol funkcija yra tolydi, gali būti tik baigtinis skaičius taškų, kuriuose išvestinė nėra apibrėžta. Visuose kituose taškuose funkcija vis tiek turėtų būti graži ir glotni. Kitaip tariant, funkcija gali zigzagu judėti tik tam tikrą kiekį kartų.

Iš tikro, 1806 m. prancūzų matematikas ir fizikas André-Marie Ampere pareiškė, kad įrodė tai ir dešimtmečius jo samprotavimai nebuvo ginčijami. Bet tada pasirodė Vejerštrasas – ir jis atrado funkciją, kuri, anot Ampero įrodymo, turėjo būti neįmanoma: ji visur buvo tolydi, tačiau niekur nebuvo diferencijuojama. Tai atliko, sudėdamas be galo daug į bangas panašių „kosinusinių“ funkcijų. Kuo daugiau narių jis pridėjo, tuo labiau jo funkcija darėsi zigzago formos 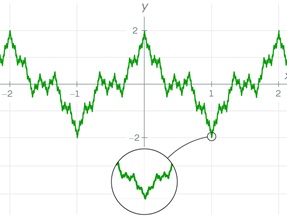– Vejerštraso funkcijos grafikas kol galiausiai ji staigiai keitė kryptį kiekviename taške, savo forma primindama be galo dantytas į pjūklo dantis panašias šukas.

Daugelis matematikų šią funkciją atmetė - jie sakė, kad tai anomalija, pedanto darbas, matematiškai visai nenaudingas. Jie net negalėjo jos vizualizuoti. Iš pradžių, bandant nubraižyti Vejerštraso funkcijos grafiką, tam tikrose srityse jis atrodo glotnus, tačiau priartinus vaizdą pamatoma, kad tos sritys taip pat yra dantytos ir kad su kiekvienu papildomu didinimu jos tampa vis labiau dantytos ir elgiasi „blogai“ (matematikai tai vadina „patologija“).

Tačiau Vejerštrassas neabejotinai parodė, kad nors jo funkcija neturi trūkių, ji niekada nėra diferencijuojama. Tam jis pirmiausia peržvelgė „tolydumo“ ir „diferencijuojamumo“ apibrėžimus, kuriuos prieš kelis dešimtmečius suformulavo matematikai Augustin-Louis Cauchy ir Bernard Bolzano. Tie apibrėžimai rėmėsi neaiškiais, paprastais aprašymais ir nenuoseklia notacija, todėl juos buvo lengva klaidingai interpretuoti. Taigi Vejerštrasas juos perrašė, naudodamas tikslią kalbą ir konkrečias matematines formules (ir būtent jis pristatė epsilon-delta apibrėžimą ir jį panaudojo ją kaip pagrindą savo tolydumo ir diferenciacijos apibrėžimams).

Tada jis sugebėjo parodyti, kad jo funkcija atitinka tą griežtesnį tolydumo apibrėžimą. Tuo pat metu jis taip pat įrodė, kad kiekviename taške jo naujas formalus funkcijos išvestinės apibrėžimas niekada neturi baigtinės vertės; jis visada „sprogsta“ iki begalybės - kitaip tariant, tolydumas nereiškia diferenciacijos. Jos funkcija iš tikro buvo tokia monstriška, kaip to ir bijojo matematikai.

Įrodymas pademonstravo, kad skaičiavimas nebegali remtis geometrine intuicija, kaip darė jo autoriai. Tai įvedė naują šios srities standartą, pagrįstą kruopščia lygčių analize. Matematikai buvo priversti sekti Vejerštraso pėdomis, toliau tobulindami funkcijų apibrėžimus, supratimą apie tolydumo ir diferenciacijos ryšį bei išvestinių ir integralų skaičiavimo metodus. Vėliau tai išaugo į atskirą matematikos sritį, žinomą kaip matematinė analizė, kurios vienu pradininkų laikomas Vejerštrasas.

Tačiau tos funkcijos palikimas gerokai peržengia skaičiavimo ir analizės pagrindus. Ji atskleidė, kad matematika pilna pabaisų: iš pažiūros neįmanomos funkcijos, keisti objektai (o tai vienas iš ankstyviausių fraktalo pavyzdžių), neįprasta elgsena. Be to paaiškėjo, kad ji turi ir daug praktinių pritaikymų. 20 a. pradžioje fizikai norėjo tyrinėti Brauno judėjimą – atsitiktinį dalelių judėjimą skystyje ar dujose. Kadangi šis judėjimas yra pastovus, bet ne glotnus, nes jam būdingi greiti ir be galo maži svyravimai, tokios funkcijos kaip Vejerštraso puikiai tiko jam modeliuoti. Panašiai tokios funkcijos buvo naudojamos modeliuojant neapibrėžtumą, kaip žmonės priima sprendimus ir prisiima riziką, taip pat sudėtingą elgesį finansų rinkose.

K. Vejerštrasas ją apibrėžė kaip Furjė eilutę:
Weierstrass function
kur 0 < a < 1; b - teigiamas nelyginis skaičius; ir ab > 1 + 3*p/2

Minimali tas sąlygas tenkinanti b reikšmė yra 7.

¹⁾ Christianas Volfas (Christian von Wolff, 1679-1754) - vokiečių filosofas, teisininkas ir matematikas, M. Lomonosovo mokytojas, gimęs Vroclave. Apkaltintas ateizmu, turėjo palikti Prūsiją, 1724-40 m. dėstė filosofiją Marburgo un-te, kur 1736-39 m. jo mokiniais buvo M. Lomonosovas. Tada grįžo į Prūsiją, nuo 1743 m. Halės un-to rektorius. Susistemino Leibnico filosofiją, kurio pagrindu sukūrė racionaliąją volfizmo šaką, Vokietijoje dominavusią 18 a. viduryje. Jis filosofiją skirstė į teorinę (ontologiją, išskiriant tris ypatingas metafizikas apie sielą, pasaulį ir Dievą: racionaliąją psichologiją, račionaliąją kosmologiją ir racionaliąją teologiją) ir praktinę (etiką, ekonomiką ir politiką). Parašė kelias instrukcijas matematikai, paveikusias matematikos dėstymą.

²⁾ Karlas Vejerštrasas (Karl Theodor Wilhelm Weierstrass, 1815-1897) – vokiečių matematikas, „šiuolaikinės matematinės analizės tėvas“. 1873 m. išrinktas išrinktas Berlyno un-to rektoriumi. Jis formalizavo funkcijos tolydumo apibrėžimą, įrodė tarpinės reikšmės (Bolcano-Koši) teoremą bei Bolcano-Vejerštraso teoremą (apie konverguojančios sekos egzistavimą), kurią panaudojo tolydžių funkcijų uždarame intervale analizei. Jo darbai žymiai praturtino matematinę analizę, variacinį skaičiavimą, diferencialinę geometriją ir tiesinę algebrą. Matematikoje siekė aiškumo ir griežtumo.
Jo garbei pavadintas krateris Mėnulyje.

³⁾ Aloisas Hiofleris (Alois Höfler, 1853-1922) – austrų filosofas. Jis studijavo matematiką Vienos un-te, kuriame vėliau ir dėstė (1907 m. profesorius). Jis dėmesį sutelkė logikai ir psichologijai, o taip pat fizikos ir matematikos mokymo didaktikai. Jo svarbesni darbai: „Filosofinė propedeutika. 1 dalis: Logika“ (1890), „Nepriklausomos tikrovės“ (1907), „B. Bolcano begalybės paradoksai“ (1921) ir kt.

⁴⁾ Leonardas Nelsonas (Leonard Nelson, 1882-1927) – vokiečių matematikas, filosofas, psichologinės krypties neokantizme vadovas, neofrizinės mokyklos neokantizme įkūrėjas, buvęs socialistinių pažiūrų ir įsteigęs socialdemotratų atskilusią ISK lygą. Buvo D. Hilberto draugu. Įrodė bendros pažinimo teorijos neįmanomumą. 1908 m. jis kartu su Kurtu Grelingu sukūrė Grelingo-Nelsono paradoksą ir susijusią autologinių žodžių idėją. Išpopuliarino „Sokrato metodą“ diskusijose. Buvo vegetaru ir pasisakė už gyvūnų teises.