Mazgai ir mazgų teorija
Tai įžanga straipsniui Revoliucija mazgų teorijoje
Pastaba: Ši įžanga nėra minėto straipsnio dalimi...
Mazgų teorija daug kuo naudinga, o jos tyrimo objektas mums gerai žinomas su jais susipažinęs kiekvienas, bandęs atraizgyti mazgą (batų raištelio ar valo žūklės metu). O ir istorija jų ilga: perverto vilko danties (matyt, karoliaus dalies) amžius yra 300 tūkst. m. Gal akmens amžių netgi geriau būtų vadinti virvelių amžiumi.
Taigi, mazgai, kaip ir sukabinimai (angl. link) nuo senų laikų buvo kultūros dalis. Jie buvo užrišami, kad padėtų
ką nors atsiminti. Keli užrišti mazgai galėjo nurodyti skaičių. Todėl netgi kažkiek keista, kad matematiniai klausimai apie
mazgus nebuvo keliami iki pat 19 a. Vienu galimu to paaiškinimų gali būti tai, kad iki tol nebuvo suformuluotos topologinės
sąvokos. Kita priežastis matematiko mazgas yra kitoks nei darbininko ar jūreivio, nes neturi palaidų galų;
mazgas yra uždaras apskritimas (arba toras) trimatėje erdvėje.
O sukabinimas (angl. link) yra baigtinis kartu suraizgytų atskirų mazgų rinkinys (jo pavyzdžiu gali būti
Boromėjų žiedai), kuriame atskiras mazgas yra sukabinimo komponentas.
Ankstyviausia svarbesnė teorema šioje srityje liečia sukabinimus: 1833 m. K. Gausas parodė, kad persipynimų skaičių (ką šiandien vadiname dviejų mazgų sukabinimų kiekiu) gali būti paskaičiuotas integralo pagalba (Gauso integralas suranda laipsnį atvaizdavimo iš toro, parametrizuojančio sukabinimą, į dvimatę sferą). Greičiausiai Gausas bandė rasti mažiausią dangaus sferos sritį (zodiaką) į kurį gali būti suprojektuotos dviejų dangaus kūnų orbitos.
Esminiu mazgų teorijos uždaviniu yra mazgų klasifikacija. Gauso mokinys J.B. Listingas5) priartėjo prie jos: straipsnyje Vostudien zur Topologie (1847), kuriuo buvo įvestas topologijos terminas, jis panaudojo polinomus kombinatoriškai koduojant mazgų diagramas, taip tikėdamasis pasiekti praktinių skaičiavimų galimybę. Jis įrodė labai nedaug, tačiau pademonstravo, kad aštuoniukė (kartais vadinama Listingo mazgu yra izotopinė savo veidrodiniam atspindžiui.
Dž. Maksvelas buvo P. Teto studijų draugas Edinburgo akademijoje. Jo monumentalus veikalas apie elektromagnetizmą (1891) panaudojo nemažai J. Listingo topologinių idėjų. Jis taip pat paaiškino giluminį Gauso sukabinimo integralo fizikinį taikyma: Jei mazgas yra laikomas laidu, kuriuo teka elektros srovė, tada integralas išreiškia darbą indikuojant magenetinį lauką jai tekant į kitą mazgą.
O matematinė mazgų teorija prasideda 1867 m. kartu jau primiršta sūkurine atomo
teorija (Vortex theory), turėjusia paaiškinti: a) atomų stabilumą; b) jų įvairovę; c) atomų vibracines savybes, kurias rodo spektrinės linijos.
Stebėdamas draugo fiziko P. Teto leidžiamus cigaro dūmų žiedus, lordas Kelvinas2)
stebėjosi šių stabilumu ir vibravimu. Jis atomus įsivaizdavo kaip eterio sūkurius. Iš kur
tada atsiranda atomų įvairovė? 1867 m. straipsnyje Karališkai draugijai teigė:
[ Pastaba: Alotropija savybė turėti kelias būsenas ar formas ]
Po to, kai H. Helmholcas parodė, kad uždara orbita pastoviame vienalyčiame skystyje negali būti nei sukuriama, nei sunaikinama, Kelvinas pasiūlė hipotezę, kad atomai yra amžini sumazgyti sūkuriukai besisukantys eteryje. Tai Tetą paskatino tiek moksliniams, tiek filosofiniams apmąstymams. Jis rašė (1876): Tad ši sukimosi savybė gali būti pagrindu viskam, ką mūsų jutimai priima kaip materiją. Tik jis skundėsi: Deja, atrodo neįmanoma mums sukurti, net su tokiais netobulais fluidais kaip oras ar vanduo, sudėtingesnį sūkurį nei paprastas apskritimas.
Pirmiausia reikėjo palyginti mazgus, tai P. Tetas ėmėsi klasifikuoti mazgus. Sūkurinė atomo teorija netrukus nuėjo į istoriją, tačiau mazgų iki 10-ies susikryžiavimų klasifikavimas bei P. Teto suformuoti teiginiai (kai kurie įrodyti visai neseniai) pasitarnavo mazgų teorijos susiformavimui.
Mazgų pavaizdavimui galime paimti virvelę ir užmegzti mazgą:
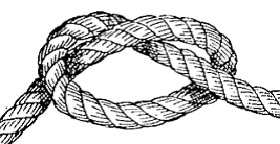
Tokio mazgo, paėmus virvelę už galų ir jų nepaleidžiant, niekaip neatriši. Tai galima padaryti tik paleidus vieną galą arba perkirpus virvelę. Tad čia ir iškyla klausimas kaip teoriškai nustatyti, kuriuos mazgus galima atmezgioti, o kurių ne.
Kad nereiktų virvutės laikyti už galų, galime juos sujungti. Taip gausime paprasčiausius mazgus: trilapį ir jo veidrodinį atspindį:

Taigi, mazgus galime vaizduoti mazgų diagramomis. Belieka nustatyti, kada dvi diagramos vaizduoja tą patį mazgą. Kad tai įsitikintume, turime vieną diagramą suvesti į kitą, kas ne taip paprasta, kaip atrodo, pvz., P. Teto lentelėse buvo du 10-mt kartų susikryžiuojantys mazgai, kurių tapatumą K.A. Perko1) įrodė tik 1974 m. Tačiau dar sunkiau įrodyti, kad du mazgai skirtingi, t.y. niekaip vienos diagramos negalima suvesti į kitą. Tai pagrindinė mazgų teorijos problema, kuri iki galo dar neišspręsta. Dalinis sprendimas rasti mazgų invariantus, kuriuos galima apibrėžti diagramomis ir kurie kitose diagramose yra tokie patys.
Reidemeisterio ėjimai
To paties mazgo perėjimus nuo vienos mazgų diagramos prie kitos galima suskirstyti į kelis pagrindinius ėjimus. 20 a. 3-me dešimtm. K. Reidemeisteris įvedė 3 pagrindinius veiksmus (ėjimus):
R1 susukti / atsukti (twist / untwist ):

R2 užstumti / nustumti (poke / unpoke ):
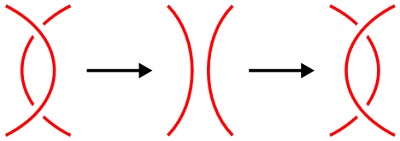
R3 slinkti (slide):
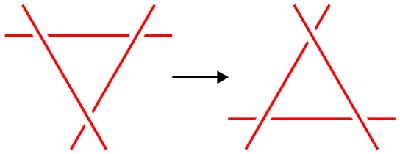
arba (vaizdžiau, irgi R3):
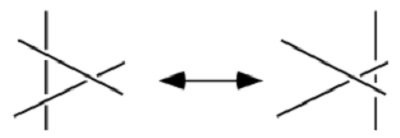
Juos dar papildykime trivialiu patampymo veiksmu R0:
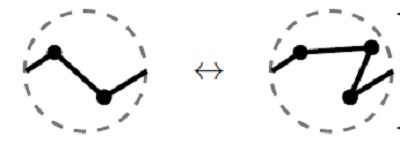
Reidemeisterio teorema
Pvz.,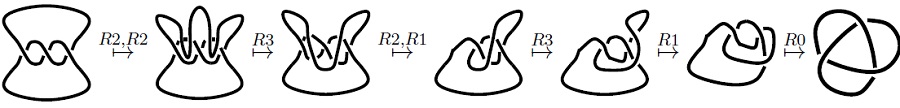

Pritaikymas
Mazgų teorija turi praktinių pritaikymų. Vienas jų gana matematiškas chaotinių srautų tyrimai. Įdomesnis yra taikymas DNR, prasidėjęs 1985 m. V. Joneso seminare Ženevose, kur buvo nagrinėjami operatorių algebros klausimai. Vienas klausytojų pastebėjo, kad aptariami elementų dėsniai pasireiškia ir kasų teorijoje. Kartu bevystant tas idėjas susiformavo nauja mazgų daugianarių teorija, pritaikyta tiriant, kaip DNR molekulės išsinarplioja, kai dalijasi.
Mazgai atsispindėjo ir mene. Pvz., J. Robinsonas3), panaudodamas Boromėjų žiedus*), sukūrė įvairių skulptūrų.
Bakterijos atsimazgymas
Prisimenate Gordijaus mazgo istoriją? Perkirsti mazgą gali būti paprasčiausias būda jį atraišioti. Įdomu,
kad panašiai savo DNR išpainioja ir Escherichia coli bakterija, kaip 2017-ais nustatė Kalifornijos un-to mokslininkai.
Ši inkstų bakterija gali sukelti žarnyno ligą, tačiau ji yra ir patogi bandymų žiurkė. Jos DNR yra uždaras
ciklas, tačiau jis gali būti susiraizgęs. Ir jei meškeriojate, puikiai žinote, kaip gali būti sunku išnarplioti susipainiojusį valą!?
Dalijantis DNR, reikia sukurti tikslų ankstesnės kopiją gaunant du uždarus ciklus. Tam panaudojamas enzimas
topoisomerase IV, kuris atkerta DNR fragmentą, leidžia ciklui išsinerti pro spragą ir vėl susiuva DNR.

Ar tvirtai laikys mazgas?
Buriavime, alpinizme, statybose susiduriame su mazgais, iš kurių vieni tvirtesni nei kiti. Pvz., bet kuris jūreivis žino,
kad vienas mazgas labiau tinka burėms pritvirtinti, o kitas prišvartuoti laivą prie kranto. Tačiau priežastis, kodėl vieni
 mazgai patvaresni nei kiti, nebuvo aiškiai suprantama. Tačiau dabar MIT matematikai ir inžinieriai sukūrė matematinį
modelį, leidžiantį nuspėti, koks bus mazgo patvarumas, remdamiesi pagrindinėmis mazgų savybėmis, tarp kurių yra susikirtimų
kiekis ir krypties, kuria mazgas suksis, kai mazgas bus sutraukiamas. Straipsnis buvo paskelbtas 2020 m. sausio 3 d. Science žurnale.
mazgai patvaresni nei kiti, nebuvo aiškiai suprantama. Tačiau dabar MIT matematikai ir inžinieriai sukūrė matematinį
modelį, leidžiantį nuspėti, koks bus mazgo patvarumas, remdamiesi pagrindinėmis mazgų savybėmis, tarp kurių yra susikirtimų
kiekis ir krypties, kuria mazgas suksis, kai mazgas bus sutraukiamas. Straipsnis buvo paskelbtas 2020 m. sausio 3 d. Science žurnale.
2018-ais M. Kolle grupė tamprias skaidulas, kurios keičia spalvą ištempiant ar suspaudžiant. Iš tokių skaidulų suvyta virvelė tempiant ją keičia atspalvius ir ypač tose vietose, kur tempimas ar spaudimas yra didžiausi. Ir kai M. Kolle, kuris yra mechaninės inžinerijos profesorius, darė pranešimą, salėje buvęs matematikos profesorius J. Dunkelis iškėlė idėją o ar negalima spalvų keitimo panaudoti tiriant mazgų stabilumą.
Mazgai jau senai domina matematikus, tačiau matematinė mazgų teorija atmeta viską, kas susiję su mechanika. Ir tiedu profesoriai nusprendė išsiaiškinti, kas nulemia mazgų stabilumą. Jie naudojo M. Kolle skaidulas rišant įvairiausius mazgus, įtraukiant trigubą mazgą ir aštuoniukės formos mazgą, kurie buvo gerai žinomi M. Kolle, esančiam užkietėjusiu buriuotoju bei J. Dunkelio grupės alpinistams. Jie fotografavo kiekvieną giją, nustatydami, kur ir kada skaidula keitė spalvą, traukiant virvutę.
Tada gautus duomenis panaudojo sudarydami matematinį modelį, o paskui naudojo tą modelį imituodami tikrovėje rištus mazgus. Tada bandymų duomenis sulyginę su tomis simuliacijomis nustatė, kad spalvų deriniai beveik sutapo.
Tada tyrinėtojai imitavo sudėtingesnius mazgus aiškindamiesi, kurie jų patiria didesnius poveikius. Ir galiausiai, suklasifikavus mazgus pagal jų tvirtumą, buvo imta aiškintis, kodėl vieni mazgai stabilesni už kitus. Tam jie nusibraižė diagramas gerai žinomiems mazgams (bobiškam, tiesioginiam, vagies,...) bei sudėtingiems (plokščią, cepelino, Alpių drugelio, ...). Lygindami diagramas tyrinėtojai nustatė pagrindines taisykles arba charakteristikas, kurios lemia mazgo stabilumą. Vertinant bendrai, mazgas tuo patvaresnis, kuo mažiau susikirtimų turi, o taip pat mažiau sukinio fliuktuacijų pokyčių krypties pasikeitimų pereinant nuo vieno segmento prie kito. Taip pat nustatyta, kad mazgas gali būti tvirtesnis, kai turi daugiau apsukimų, kai dvi lygiagrečios vijos sukasi priešingomis kryptimis.
|
|
*) Boromėjai Italijos giminė Milane, kurios herbe buvo pavaizduoti šie žiedai
(daugiau apie jų taikymus žr. >>>>>).
Jos įtaka mieste bei Madžorės ežero apylinkėse išlikusi iki šiol. Iš jos kilę 7-i kardinolai. Savo kilmę išveda nuo
krikščionių kankinės Justinos iš Padujos (nužudytos apie 303 m.), kas nėra patvirtinta. Tarp 14 ir 17 a. jie sugebėjo
išlaikyti beveik nepriklausomą Boromėjų valstybę Milano hercogystėje. Jos gyvavimas nutrauktas 1797 m. Milaną
užėmus Napoleonui Bonapartui, tad Boromėjų nuosavybė išlikusi tik Boromėjų salose Madžorės ežere.
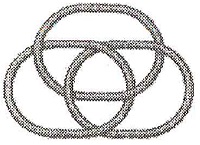
Boromėjų žiedai - trys uždaros kreivės (žiedai) trimatėje erdvėje, topologiškai sujungtų taip, kad
neatsiskiria, tačiau išsiskiria į dvi nesujungtas uždaras kreives, jei perkerpama (arba pašalinama) kuri nors iš kreivių
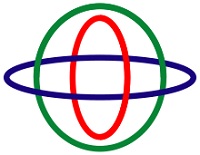 (Brunono sankabos). Jie yra paprasčiausias Brunono sankabos pavyzdys. Žiedai pasižymi įdomia savybe, kad
neįmanoma gauti tokią sankabą iš geometriškai idealių apskritimų (t.y. jų nelankstant) mat, tarus, kad du apskritimai
susiliečia 2-iuose susikirtimo taškuose, tada jie turi rastis arba vienoje plokštumoje, arba ant sferos. Abiem atvejais
trečiasis apskritimas privalo kirsti tą plokštumą arba sferą 4-iuose taškuose ir nebūti jose, - kas yra neįmanoma. Tačiau tai
galima padaryti su trimis elipsėmis, kurių ekscentricitetas gali būti kiek norima mažu.
(Brunono sankabos). Jie yra paprasčiausias Brunono sankabos pavyzdys. Žiedai pasižymi įdomia savybe, kad
neįmanoma gauti tokią sankabą iš geometriškai idealių apskritimų (t.y. jų nelankstant) mat, tarus, kad du apskritimai
susiliečia 2-iuose susikirtimo taškuose, tada jie turi rastis arba vienoje plokštumoje, arba ant sferos. Abiem atvejais
trečiasis apskritimas privalo kirsti tą plokštumą arba sferą 4-iuose taškuose ir nebūti jose, - kas yra neįmanoma. Tačiau tai
galima padaryti su trimis elipsėmis, kurių ekscentricitetas gali būti kiek norima mažu.
Jei perkirpsime Boromėjų žiedus, gausime vieną kasos iš trijų juostų pynimo iteraciją.
Boromėjų žiedai sutinkami skirtingose pasaulio vietose išraižyti ant senovės skandinavų akmenų (valknuto, arba kitaip Odino mazgo,
forma7), 7 a.), romėnų mozaikose, ankstyvajame budistų mene, Japonijos ir Indijos šventyklose.
Krikščionybėje jie naudoti simboliniam vienybės Trejybėje pavaizdavimui.
Pvz., A.N. Didronas savo knygoje Krikščioniško meno istorija Viduramžiais, 1843 m. atgamino piešinį iš dingusio per gaisrą 13 a. rankraščio ir jis,
kaip ir kiti, tvirtino, kad Trejybės atvaizdavimas
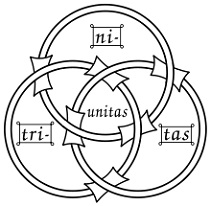 trimis lygiais apskritimais Trejybės Rojaus 33 skyriuje buvo įkvėptas panašių pavaizdavimų.
trimis lygiais apskritimais Trejybės Rojaus 33 skyriuje buvo įkvėptas panašių pavaizdavimų.
Pirmasis veikalas apie mazgų teoriją, kuris įtraukė boromėjų žiedus, buvo Peter Taito mazgų katalogas Apie mazgus (1876), o juos išpopuliarino M. Gardneris, 1961 m. Scientific American pristatęs Seiferto paviršius jiems. Tarptautinė matematikos sąjunga 2006 m. boromėjų žiedus pasirinko savo naujuoju logotipu.
1) Keneth A. Perko (1941-2002) JAV teisininkas ir, iš dalies, matematikas.
Išplito legenda, kad šis teisininkas, be jokio matematinio išsilavinimo, iš nuobodulio ofise raizgė virvę pagal knygą, ir netikėtai aptiko, kad mazgas 10161 transformavosi į 10162.
Iš tikro, tai jis gavo matematinį išsilavinimą (nors ir negynė daktarinės disertacijos), klausydamas žinomų mazgų teorijos topologų (R.H. Fox'o4), Milnor'o, Neuwirth'o, Stallings, Trotter'io, Tucker'io) paskaitų. R. Foksas pasiūlė Perko perskaityti paskutinį Reidemeisterio knygos skyrių ir pažiūrėti, ar galima nustatyti, kaip jis paskaičiavo tuos jungiančius skaičius. Tai atvedė prie kai kurių įdomių rezultatų ir Perko tapo žinomu specialistu šioje srityje.
Vėliau jis studijavo teisę, tačiau liko susidomėjęs mažų matų topologijos klausimais ir dažnai skelbė straipsnius.
2) Viljamas Tomsonas (William Thomson, 1st Baron Kelvin, 1824-1907) britų mokslininkas, teorinės fizikos specialistas, ir mechanikas-inžinierius. Prisidėjo vystant matematinę elektros teoriją bei suformulavo pirmąjį ir antrąjį termodinamikos dėsnius (taip pat žr. >>>>>).
Gausi jo darbų tematika: termodinamikos ir hidrodinamikos tyrinėjimai, bangų teorija, termoelektros teorija, kurioje yra Tomsono efektas (elektros srovės pernešama šiluma), tamprumo tyrinėjimai, darbai dinaminės geologijos srityje ir kt.
Žinomas ir daugeliu daugeliu praktinių išradimų: veidrodinio galvanometro, onduliarotiaus su sifoniniu rašalų pateikimu, jūrų kompaso, elektrometrų ir daugelių kitų elektros matavimo prietaisų, tarp kurių išskirtiniausias amper-svarstyklės, taikomos elektros prietaisų patikrai.
Jis žinomas evoliucijos teorijos kritika. Pagal savo Saulės amžiaus paskaičiavimus, kurioje, jo nuomone vyksta degimo procesas, teigė, kad istorinio laiko nepakanka gyvūnų pasaulio evoliucijai. 1903 m. atrastas radioaktyvus skilimas nepakeitė jo nuomonės apie Saulės amžių jis Žemės amžių laikė esant 20-40 mln. m.
1870-1890 m. tarp britų fizikų buvo labai populiari sūkurinė atomo teorija (atomas sūkurys eteryje), kurią palaikė ir Tomsonas. O kartu su P. Tetu padėti pagrindai mazgų teorijai.
Iš jo knygų žinomiausia yra Apie gamtos filosofiją (1883), išdėstanti teorinės fizikos mechaninius pagrindus.
Jo garbei pavadintas temperatūros vienetas kelvinas (K)
3) Džonas Robinsonas (John Robinson, 1935-2007) britų skulptorius, Bradshaw fondo vienas steigėjų (ir buvo archeologijos bei antropologijos entuziastas). Buvo 1988 m. britų Olimpinio komiteto oficialiu skulptoriumi; sukūrė nemažai sportinės temos skulptūrų (Gimnastas yra Šveicarijos Lozanos Olimpiniame muziejuje). Nuo 1975 m., kai klausant Mocarto muzikos kilo mintys apie abstrakčias formas, abstraktaus tipo skulptūrų sukūrė per 100. Jomis išreiškė ir mokslines koncepcijas; tarp jų pasižymėjo ir matematikos idėjų (fraktalų, boromėjų žiedų ir kt.) vizualizacija.
4) Ralfas Foksas (Ralph Hartzler Fox,1913-1973 ) amerikiečių matematikas, Prinstono un-to profesorius, prisidėjęs modernizuojant mazgų teoriją. Jo vardu vadinamas mazgų n-spalvinimas, Foksi-Artino lankas. Taip pat sįvedė kelis svarbius terminus į mazgų teoriją. Buvo Go žaidimo entuziastas.
5) Johanas Benediktas Listingas (Johann Benedict Listing,
1808-1882) vokiečių matematikas, fizikas. Užsiėmė ir astronomija, meteorologija, optika, spektroskopija, elektromagnetizmu.
1845 m. išleidžia puikią Psichologinę optiką, kuriai iliustracijas parengė pats. 1847 m. straipsnyje [J.B. Listing,
Vorstudien zur Topologie// Goettingen Studien 2, 1848, p.811875] pirmąkart įvedė topologijos sąvoką, nors šį terminą
susirašinėdamas naudojo ir anksčiau. 1858 m. nepriklausomai nuo A. Miobuso6) atranda
Mobiuso juostą.
6) Augustas Mobiusas (August Ferdinand Möbius, 1790-1868) vokiečių matematikas, mechanikas ir astronomas teoretikas. Žinomas daugelio puikių darbų apie geometriją (ypač projektyviąją, kurioje įvedė homogenines koordinates), matematinę analizę ir skaičių teoriją. Daug geometrinių atradimų išdėstė Baricentriniame skaičiavime (1827). 1858 m. beveik vienu metu su I. Listingu nustatė vienpusio paviršiaus (Mobiuso juostos) egzistavimą. Mechanikos srityje daugiausia dėmesio skyrė statikai, paskelbė dvitomį Statikos vadovą (1837). Nuo 1848 m. buvo Leipcigo observatorijos direktoriumi, rūpinosi jos pertvarkymu ir aprūpinimu. Žinomiausias jo darbas šioje srityje Dangaus mechanikos elementai (1843). Jo garbei pavadintas krateris nematomoje Mėnulio pusėje ir asteroidas 28516.
7) Anot mitų, kai Toras įveikė milžiną Hrungnirą , šio širdis buvo keistos formos tarsi trys tarpusavyje susipynę trikampiai.
Topologija
Trikampiai skaičiai
Kaip pakuoti standžiau?
Žmonės prieš kompiuterius
Revoliucija mazgų teorijoje
Kirmgrauža tarp matematikos sričių
Aukso gysla Ramanadžano lygtims
Kaip išgyventi aukštesnius matavimus?
Mazgų teorija: juostos-nuopjovos teiginys
Kas per velnias tie pėdai topologijoje?
Mokslo ribotumas: Dievas, Giodelis ir gravitacija
Kai kurie pasiekimai 2020 m. matematikoje: išmazgymas
Moksleivis perkando I. Niutono uždavinį
Apie Tarskio skritulio kvadratinimą
Mokslininkui nereikia matematikos!
Proveržis skaičiuojant skaidinius
Diagramos, pakeitusios pasaulį
Da Vinči matematinė klaidelė
Izingo modelis įmagnetinimui
Scenoje - paprastos grupės
Kur viešpatauja chaosas?
Visata kaip kompiuteris
Matematika ir muzika
Ar viskas čia taip?
Dalyba iš nulio
Minties virusai
Matroidai
Vartiklis





